Search Space

搜索cell作为网络结构的构件。cell是包含N个结点的有序序列的有向无环图。结点$x^{(i)}$是隐藏表达（比如卷积网络的特征图），而有向边$(i ,j)$则关联着变换$x^{(i)}$的一些操作$o^{(i,j)}$。文章中假定一个cell中有两个输入节点和一个输出节点。对于卷积cell，输入节点被定义为当前层的前面两层的cell的输出。当前cell的输出是对所有中间节点使用一个压缩操作（比如拼接）得到的。

每一个中间结点基于其所有前向操作计算得到：

$x^{(j)}=\sum_{i<j}o^{(i,j)}(x^{(i)})$

搜索空间中还包含了一个特殊的零操作，表示两个节点之间没有连接。学习cell的任务缩减为学习出cell的各条边的操作类型及参数。

连续优化

O是候选操作（如卷积、最大池化、零操作等）的集合，每个操作表示将一些函数$o(\cdot)$施加到$x^{(i)}$上。为了让搜索空间连续，我们把一个特定操作的范畴选择松弛为所有可能的操作上的一个softmax:

$\overline{o}^{(i,j)}(x)=\sum_{o\in O}\frac{exp⁡(\alpha_{o}^{(i,j)})}{\sum_{o'\in O}exp⁡(\alpha_{o'}^{(i,j)})}o(x)$

对应于节点对$(i, j)$的操作混合权重被参数化为一个维度为|O|（候选操作总个数）的向量$\alpha^{i,j}$。架构搜索的任务就减少为学习一个连续变量集合$\alpha={\alpha^{(i,j)}}$。在搜索的最后，将每个混合操作$\overline{o}^{(i,j)}$用最大似然的操作代替，就可以得到离散化的网络架构。比如$o^(i,j)=argmax_{o\in O}\alpha_{o}^{(i,j)}$在下文中，用$\alpha$表示编码后的架构。

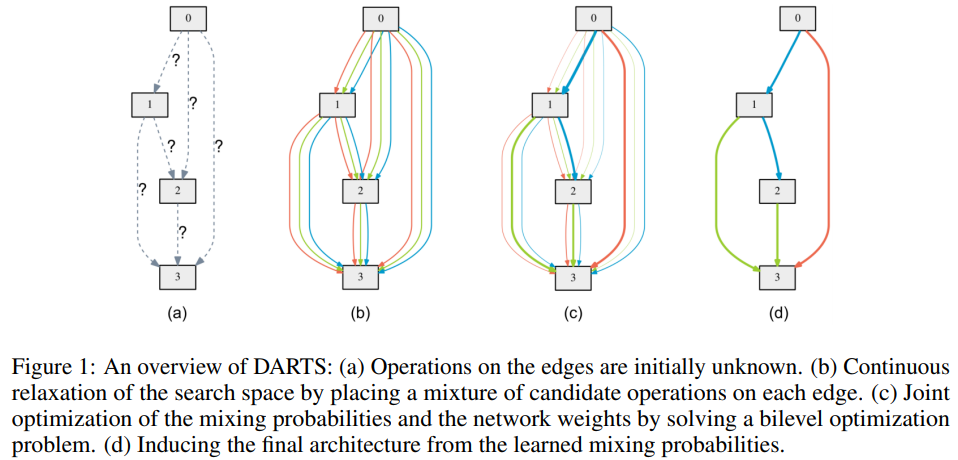
darts

DARTS的cell搜索过程概览如上图所示。该过程总结如下。最开始时cell的各条边的操作类型未知，但是可选的操作类型是预先定义的，候选操作集合中包含以下8种操作：（1）恒等连接；（2）零操作；（3）3×3 深度可分离卷积；(4) 3×3 空洞深度可分离卷积；（5）5×5深度可分离卷积；（6）5×5 空洞深度可分离卷积；（7）3×3平均池化；（8）3×3 最大池化。对于用DAG表示的cell的每条边施加一个候选操作的混合操作（混合操作是上述8种类型操作的混合，输入用8种操作进行处理，对得到的8个输出施以权重$\alpha^{(i.j)}_{o}$，然后松弛化为softmax），从而将分立的搜索空间用softmax函数松弛为连续空间，使得搜索可微分。然后通过求解一个置信优化问题对混合概率和网络权重进行联合优化，最后，将每个混合操作$\overline{o}^{(i,j)}$用最大似然的操作（也就是$i,j$结点的8条边中有着最大权重$\alpha^{(i.j)}_{o}$的那条边所对应的操作）代替，就可以得到离散化的网络架构。也就是说，训练的时候对于每两个结点之间，是8种操作都用到了，用softmax耦合为混合操作。训练完后，只保留了权重最大的那个操作。

现在目标就是将架构$\alpha$和所有混合操作中的权重$w$一起学习出来。DARTS使用梯度下降算法优化交叉检验集损失。使用$L_{train}$和$L_{val}$分别表示训练集loss和交叉检验集的loss，则优化目标是：

$\min\limits_{\alpha}L_{val}(w^{*}(\alpha),\alpha)$ $s.t. w^{*}(\alpha)=argmin_{w}L_{train}(w,\alpha)$

即找到最优结构$\alpha^{*}$使得在验证集上得到最优结果，即最小化$L_{val}(w^{*},\alpha^{*})$，并找到最优参数$w^{*}$，能够在特定结构$\alpha^{*}$上得到最优性能，即最小化$L_{train}(w,\alpha^{*})$。

网络架构梯度近似

由于昂贵的内层优化代价，精确地求出网络架构的梯度是几乎不可能的。因此，这篇文章提出了一个简单的近似方案：

$\bigtriangledown_{\alpha}L_{val}(w^{*}(\alpha),\alpha)\approx\bigtriangledown_{\alpha}L_{val}(w-\xi\bigtriangledown_{w}L_{train}(w,\alpha),\alpha)$

其中$w$是由近似算法得到的当前的权重，$\xi$是一步内层优化的学习率。这个算法的思路是使用一步训练调整得到的$w$来近似$w^{*}(\alpha)$，而不用训练解决内层优化问题直至收敛。如果w已经是内部优化的局部最优值，此时$\bigtriangledown_{w}L_{train}(w,\alpha)=0$，因此等号右边的式子会退化为$\bigtriangledown_{\alpha}L_{val}(w(\alpha),\alpha)$。

算法： algorithm

对近似的架构梯度应用链式法则可以得到：

$\bigtriangledown_{\alpha}L_{val}(w',\alpha)-\xi\bigtriangledown^{2}_{\alpha,w}L_{train}(w,\alpha)\bigtriangledown_{w'}L_{val}(w',\alpha)$

其中$w’=w-\xi\bigtriangledown_{w}L_{train}(w,\alpha)$表示一个一步前向网络的权重值。上式的第二项中包含了一个昂贵的矩阵-向量乘法，但是使用有限差分近似可以显著降低计算复杂度。使用一个很小的数值$\epsilon$，并令$w^{\pm}=w\pm\epsilon\bigtriangledown_{w’}L_{val}(w’,\alpha)$，则：

$\bigtriangledown^{2}_{\alpha,w}L_{train}(w,\alpha)\bigtriangledown_{w'}L_{val}(w',\alpha)\approx\frac{\bigtriangledown_{\alpha}L_{train}(w^{+},\alpha)-\bigtriangledown_{\alpha}L_{train}(w^{+},\alpha)}{2\epsilon}$

计算这个有限差分式只需要权重值的两个前传项和$\alpha$的两个反传项，计算复杂度从$O(|\alpha||w|)$降到$O(|\alpha|+|w|)$。

一阶近似：

当$\xi = 0$时，式(7)中的二阶导数项会消失。此时，架构梯度由$\bigtriangledown_{\alpha}L_{val}(w,\alpha)$给出，对应着假定当前的$w$与$w^{*}(\alpha)$相同然后优化交叉检验loss的情况。这会带来一些加速，但是根据实验结果显示，性能会变差。下文用一阶近似来指代$\xi = 0$的情形，用二阶近似来指代$\xi > 0$时的梯度公式。

离散架构推导

为了组成离散架构中的每一个节点，文中在该节点所有的前面节点的所有的非零候选操作中保留了top-k的最强操作。一个操作的强度被定义为

$\frac{exp(\alpha^{(i,j)}_o)}{\sum\limits_{o'\in O}exp(\alpha^{(i,j)}_{o'})}$

其实就是两个节点之间所有候选操作都施加上去，给每个候选操作都赋予权值。权值用softmax激活之后相加起来作为节点的输出，反传学习可以更新结构权值$\alpha$。最后保留权重最大的（强度最强的）k个结点与本结点的连接。在DARTS的文章中，CNN中选择k=2。

DARTS论文

具体公式推导