Motivation
目标:设计更加高效的深度神经网络,可以在资源有限的移动设备运行。
现有工作的局限性:常规的卷积基于乘法,代价较高;用二值滤波器替换卷积的工作如BNN等会带来较大的识别准确率下降。
文章思路:常规卷积本质上是一种互相关(输入图像与卷积核之间的相似度度量)。可以用更高效的相似度度量方法来替换常规卷积,使得度量中只包含代价较小的加法操作→AdderNet
AdderNet
开局公式
F: 卷积核(滤波器)(尺寸$d×d$) 当d=1时,该公式表示全连接层的计算
X:特征图
S:预定义的相似度测量方法,例如互相关中$S(x,y)=x\times y$
从上述公式出发,文章改变S,使用L1距离测量F和X的相似度,使得测量中只有加法没有乘法:
使用L1距离存在的问题及解决:
问题1:加法滤波器的输出总为负数(会影响激活函数如ReLU的使用)
解决方法:使用Batch Normalization→输出被归一化到适当的范围→CNN中的激活函数在AdderNet中也适用 (BN中存在乘法,但是数量太少可以忽略)
问题2.1:优化方法中滤波器F梯度的计算
AdderNet中计算偏微分:
所以梯度取值只有+1,0,-1。由此进行优化的方法为signSGD,但是,signSGD几乎永远不会沿着最陡的下降方向,并且方向性只会随着维数的增长而变差。
解决方法:使用另一种形式的梯度(实际上是L2范数的梯度):
问题2.2:优化方法中特征图X梯度的计算
同样使用L2范数的梯度,但是梯度值可能会在[-1,+1]的范围之外→由于chain rule,Y对X的偏导数不仅影响当前层的梯度,还会影响当前层之前的所有层的梯度→梯度爆炸
解决方法:使用HardTanh函数(HT(x))将X的梯度clip到[-1,+1]的范围。
问题3:AdderNet使用L1范数得到的Y方差更大,导致滤波器权重的梯度消失问题
假设F和X服从正太分布
CNN中有
而AdderNet中则是
实际情况中Var[F]非常小,所以$Var[Y_{AdderNet}]$会比$Var[Y_{CNN}]$大。在加法层后面会接一个BN层,大方差会导致X的梯度幅值小,经过chain rule的作用,滤波器的权重梯度幅值会越来越小。
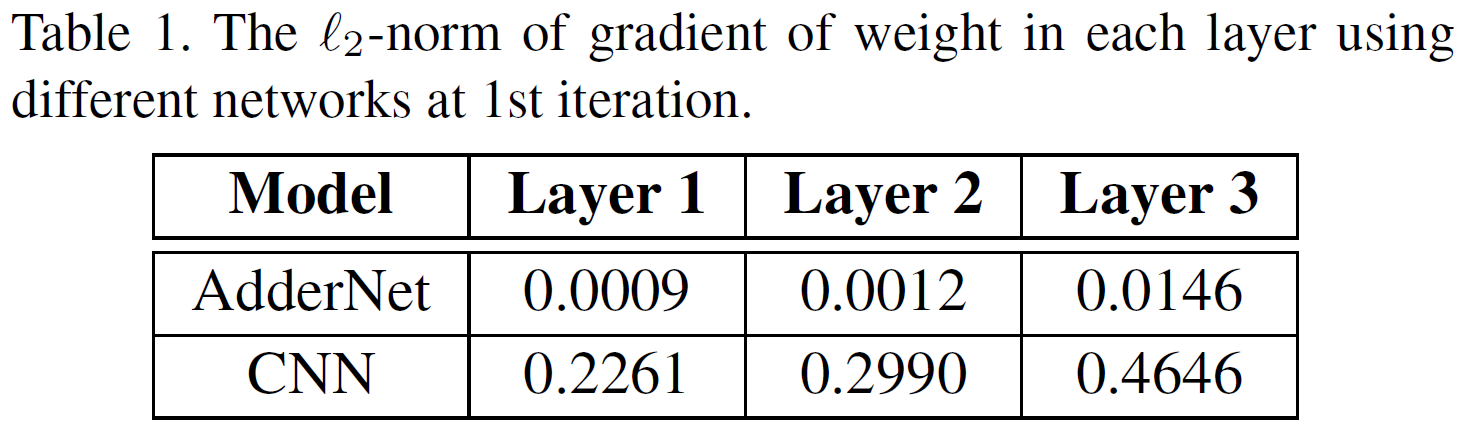
解决方法:adaptive learning rate
$l$:表示第$l$层;$\triangle L(F_{l})$第$l$层F的梯度;$\gamma$:全局学习率
局部学习率:
k:F中的元素数量,用于对L2范数求平均
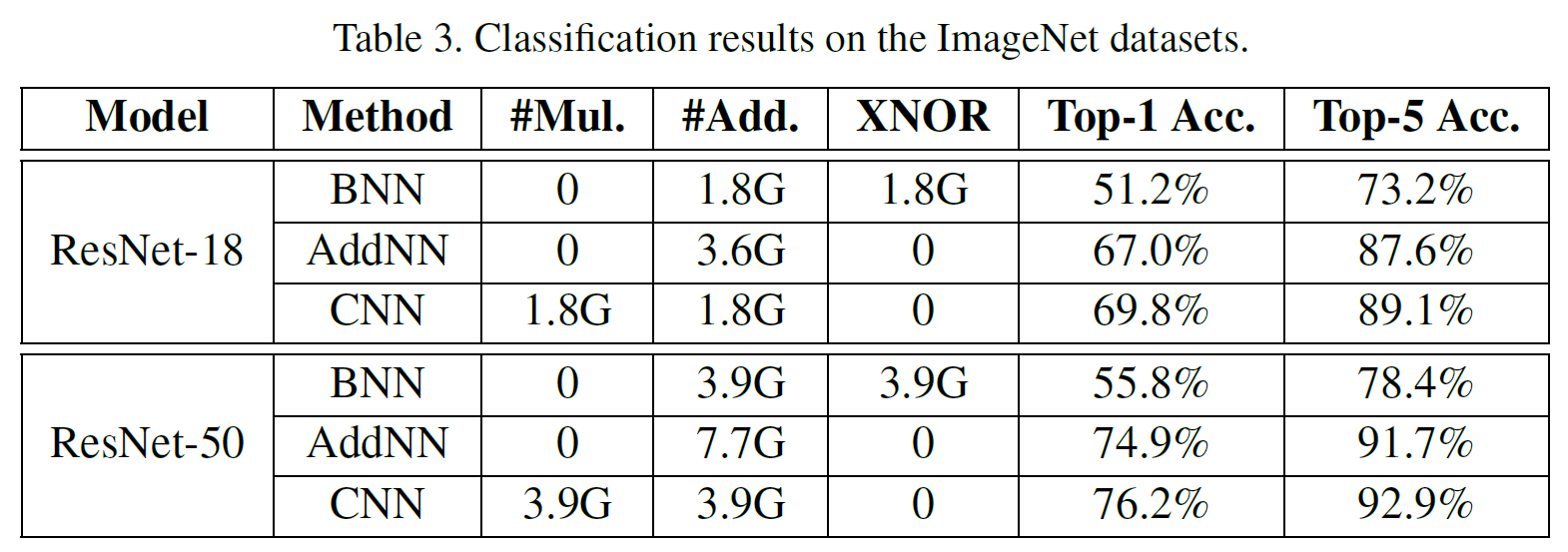
Results
在MNIST、CIFAR10、CIFAR100、ImageNet上达到与CNN相近的准确率。
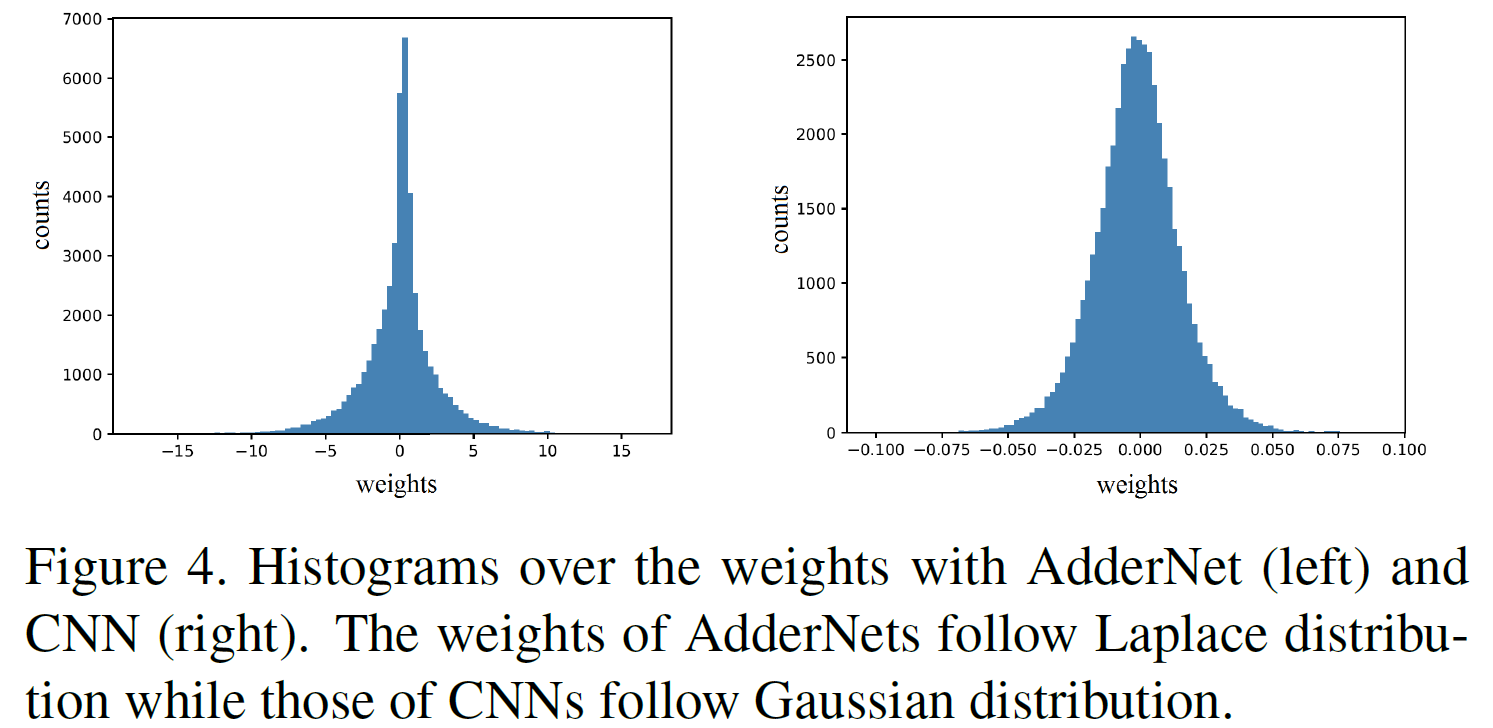
AdderNet的权重服从拉普拉斯分布,而CNN的权重服从高斯分布。
AdderNet: DoWe Really Need Multiplications in Deep Learning?