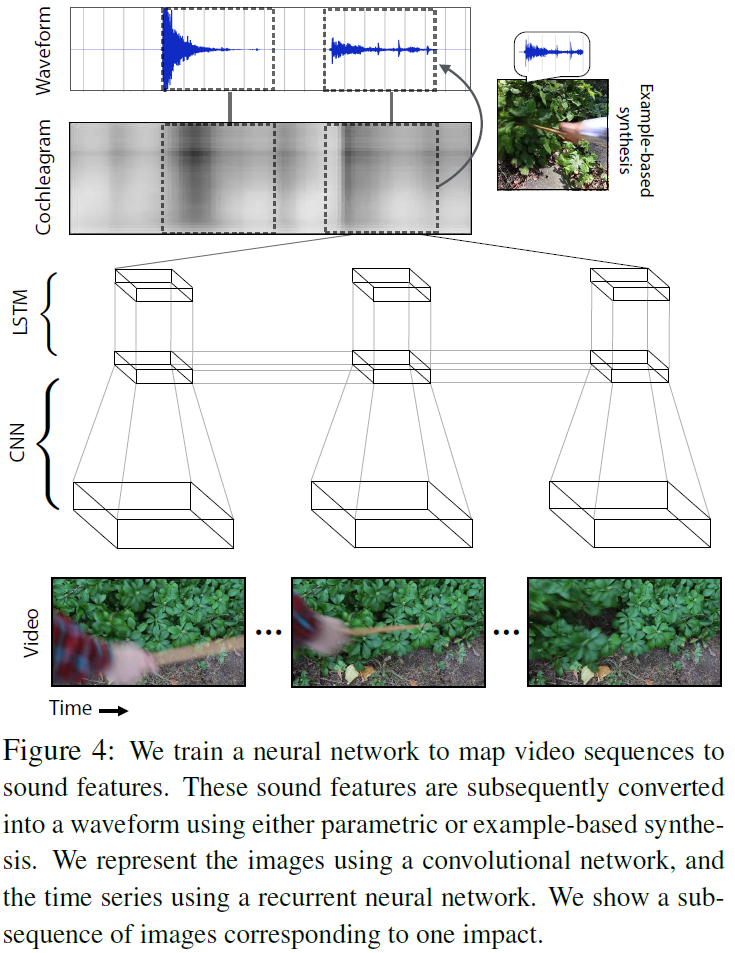
简介
现象:声音到达物体会在物体表面引起微小振动。
做法:使用物体的高速视频提取微小振动,部分恢复(造成振动的)声音。
具体:1)从一系列不同特性的物体的高速连续镜头中恢复声音;
2)使用真实和仿真数据来评测那些影响了可视化地恢复声音的因素;
3)声音恢复质量评价指标:可理解性(intelligibility)、SNR;直接对比输入和恢复出来的信号;
4)探索如何利用普通用户相机的卷帘快门(rolling shutter)从而从标准帧率视频中恢复出声音;使用所提方法的空间分辨率来可视化声音引起的振动是如何随着物体表面变化的,以之恢复物体的振动模式。
Keywords:远程声音采集;视频中的声音;可视化声学。
Introduction
描述:声音到达某物品 → 1)物品表面跟随周围介质移动 OR 2)根据其振动模式发生形变。
应用场景:声音引起物体振动的现象被用于远程声音采集,并在监视和安防方面有重要应用,如在远处窃听谈话。远程声音采集的现有方法本质上是积极(active)的,需要将一个激光束或pattern投射到振动表面。
本文观察:只需要物体的高速视频,声音引起的物体振动通常能够产生足够的视觉信号来部分恢复出该声音。
本文贡献:提出一个消极的从视频中恢复声音信号的方法。视觉上检测微小物体振动→将振动转回音频信号(使得日常物品变成潜藏的麦克风)。做法:1)使用高速摄像机将物体视频;2)在一个Complex steerable pyramid (CSP)(建立在视频上)的维度上提取局部运动信号;3)这些局部信号被对齐并取平均,得到一个单一的一维运动信号,该信号捕捉对象随时间的全局运动;4)进一步滤波和去噪,得到恢复出来的声音。
对比积极方法:恢复效果不如积极方法;但是优点有 1)对于纹理物体和光照良好的场景不需要提供积极照明;2)除了高速摄像机外无需额外的传感器或检测模块;3)无需回射或反射振动表面(区别于激光麦克风);4)没有对相对于相机的表面方向施加明显的约束;5)产生了一个声音的空间测量,可用于分析物品中声音引起的形变。
讨论:虽然声音可以穿透大多数物质,但并不是所有的物体和材料都能很好地进行视觉声音恢复。声波在材料中的传播取决于多种因素,如材料的密度和可压缩性,以及物体的形状。文章进行对照实验,测量了不同物体和材料对已知和未知声音的反应,并评估文章所提技术对于从高速视频中恢复声音的能力。
传统麦克风的工作原理是将内部膜片的运动转化为电信号。膜片的设计使其在声压下容易移动,因此它的运动可以被记录下来并解释为音频。激光麦克风的工作原理与此类似,但它测量的是一个遥远物体的运动,本质上是将物体作为一个外部膜片。这是通过记录激光对物体表面的反射来实现的。最基本的激光麦克风记录反射激光的相位,以激光波长作模得到物体的距离。激光多普勒测振仪(LDV)通过测量反射激光的多普勒频移来确定反射面速度,从而解决相位包裹的模糊性。这两种类型的激光麦克风都可以从很远的距离恢复高质量的音频,但依赖于激光和接收器相对于具有适当反射比的地面的精确定位。
Zalevsky等人通过使用失焦高速相机来记录反射激光散斑模式的变化,解决了其中的一些局限性。他们的工作允许接收器的定位有更大的灵活性,但仍然依赖于记录反射激光。相比之下,本文的技术不依赖于主动照明。
本文方法依赖于从视频中提取极其细微运动的能力,因而也与对这些运动进行放大和可视化的工作有关。这些工作侧重于小运动的可视化,而本文侧重于测量这些运动并利用它们来恢复声音。本文工作中使用的局部运动信号来自Simoncelli等人提出的Complex steerable pyramid (CSP)中的相位变化,因为这些变化被证明非常适合于视频中微小动作的恢复。然而,也有可能使用其他技术来计算局部运动信号。例如,经典的光流和点相关方法在之前的视觉振动传感工作中被成功地使用。由于本文方法的输出是单个振动物体的一维运动信号,因而能够对输入视频中的所有像素进行平均,并在千分之一像素的数量级上处理极其微小的运动。
Recovering Sound from Video
输入:物体的高速视频(1kHz~20kHz)$V(x,y,t)$
假设:物体和相机的相对运动是由声音信号$s(t)$引起的振动主导的
目标:从$V$得到$s(t)$
步骤:1)根据不同的方向$θ$和尺度$r$将$V$分解成多个空间子带;
2)计算每个像素、方向和尺度上的局部运动信号;通过一系列的平均和对齐操作将这些运动信号组合起来,为物体产生一个单一的全局运动信号;
3)对物体的运动信号使用音频去噪和滤波技术,以获得恢复出来的声音。
Computing Local Motion Signals
使用$V$的CSP表示中的相位变化来计算局部运动。
CSP:将$V$中的每一帧根据不同的方向和尺度分解成复数子带的滤波器组。该变换的基础方程是带尺度和方向的兼具余弦和正弦相位的Gabor-like小波。每一对类余弦和类正弦滤波器都可以用来分离局部小波的振幅和它们的相位。具体地说,每个尺度$r$和方位$θ$是一个复数图像,可以用幅值$A$和相位$φ$表示为:
取这个等式中计算的局部相位$φ$,从参考帧$t_{0}$(通常是视频的第一帧)的局部相位中减去它们,计算相位变化
对于较小的运动,这些相位变化近似正比于图像结构在相应方向和尺度上的位移。
Computing the Global Motion Signal
对于CSP的每个尺度$r$和方位$θ$求局部运动信号的加权平均:
求加权平均的原因:局部相位在没有太多纹理的区域是模糊的,导致这些区域的运动信号是有噪声的。CSP的振幅A给出了纹理强度的度量,因此可以通过(平方)振幅来加权每个局部信号。
对齐:
得到全局运动信号:
归一化到[-1,1]的范围。
Denoising
目标:改善全局运动信号的SNR
观察到的现象:低频的高能量噪声通常与音频不一致
方法:应用高通Butterworth滤波器(截断频率为20-100Hz)
滤除加性噪声:目标是accuracy,用spectral subtraction;目标是可理解性,用感知驱动的语音增强算法(通过计算一个贝叶斯最优估计去噪信号的成本函数,考虑到人类对语音的感知)。本文的结果是自动使用二者之一的算法来去噪的。
恢复信号的不同频率可能会被记录对象不同地调制。第4.3节将展示如何使用已知测试信号来描述一个物体如何衰减不同频率,然后在新的视频中使用该信息来均衡从同一物体(或类似物体)中恢复的未知信号。
Experiments
第一组实验测试了可以从不同物体上恢复的频率范围。通过扬声器播放线性渐变频率的声音信号,然后观察哪些频率可以通过本文技术恢复。第二组实验集中在从视频中恢复人类语言。这些实验使用了来自TIMIT数据集的几个标准语音示例,以及通过扬声器播放的人类受试者的现场语音(扬声器被一个会说话的人替换)。
Sound Recovery from Different Objects/Materials
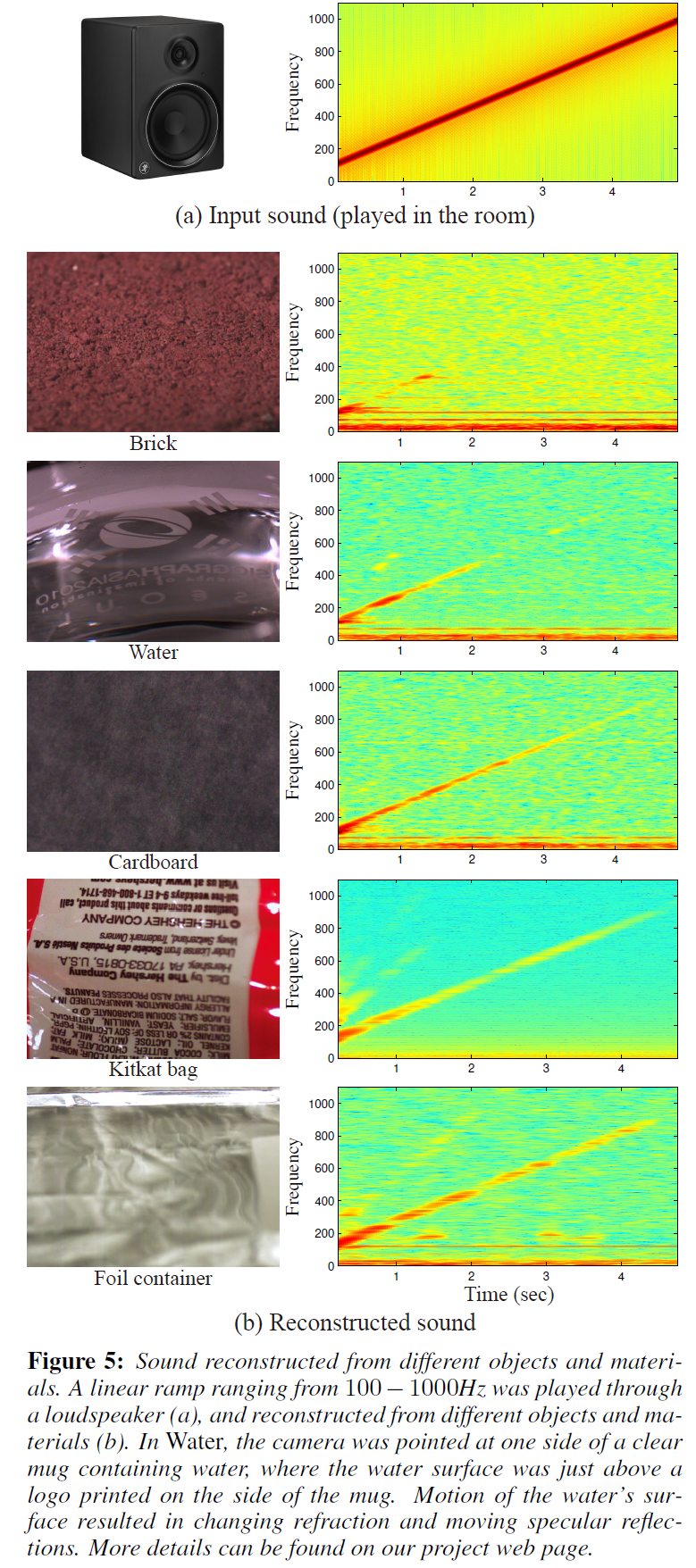
在几乎所有的结果中,恢复的信号在较高的频率中是较弱的。这是意料之中的,因为更高的频率产生更小的位移,并且被大多数材料严重衰减。然而,较高频率的功率下降不是单调的,可能是由于振动模式的刺激。毫不奇怪,较轻的物体更容易移动,比惰性的物体更容易支持更高频率的恢复。
Speech Recovery
评测指标:
(1) 评测accuracy: Segmental Signal-to-Noise Ratio (SSNR) 随时间的平均局部信噪比;
(2) 评测intelligibility: perceptually-based metric
(3) 评测恢复质量:Log Likelihood Ratio (LLR),评测恢复信号的谱形状与原始干净信号的谱形状有多接近
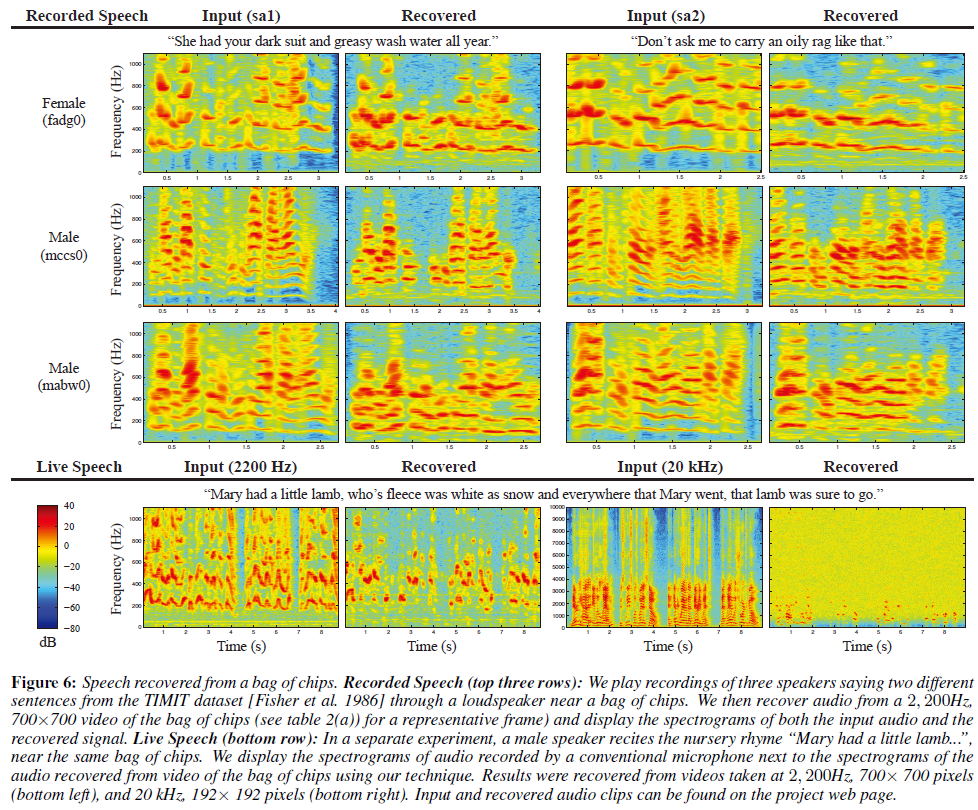
更高的帧率导致曝光时间减少,因此图像噪声更多,这就是为什么20,000FPS结果图比2200Hz时的结果噪声更大
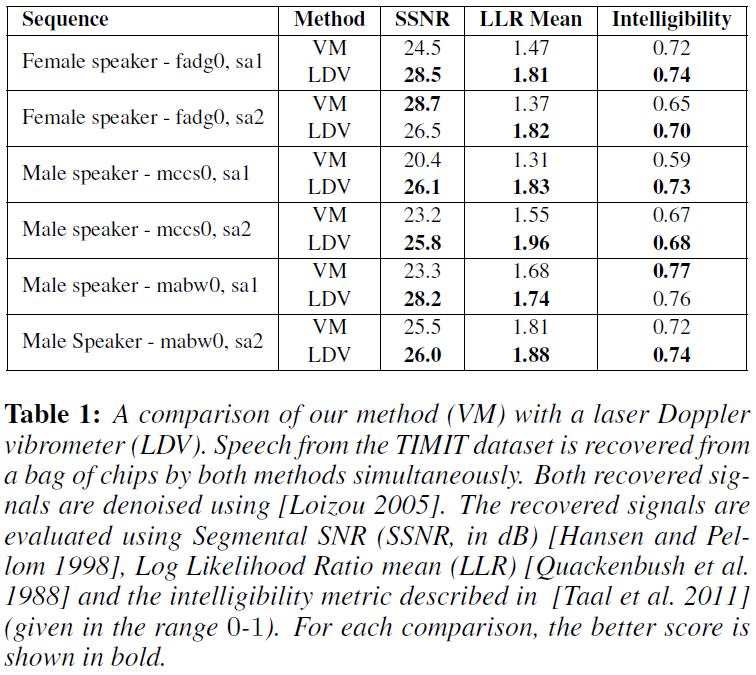
VM和LDV结果相近,而LDV需要积极照明(必须在物体上粘上一条反反射胶带以便激光从物体上反射回来回到振动计上)
Transfer Functions and Equalization
可以使用第4.1节中的斜坡信号来表征物体的(可视的)频率响应,以提高从该物体的新观测中恢复的信号质量。理论上。如果认为物体是线性系统,可以使用维纳反卷积估计与该系统相关联的复数传递函数,并且传递函数可以用来以一种最优的方式(在均方误差意义上的)解卷积新的观测信号。然而,在实践中,这种方法很容易受到噪声和非线性artifacts的影响。因此,本文描述了一种更简单的方法,首先使用训练实例(线性斜坡)的短时间傅里叶变换在粗尺度上计算频率传递系数,然后使用这些传递系数使新的观测信号相等。
转移系数是从一对输入/输出的信号的短时功率谱中提取出来的。每个系数对应于观察到的训练信号的短时功率谱的一个频率,并作为随时间变化的频率幅值的加权平均被计算。每一时刻的权值由对准的输入训练信号的短时功率谱给出。由于输入信号一次只包含一个频率,这个加权方案忽略了图2(b)中所示的倍频等非线性artifacts。
一旦有了传输系数,我们就可以用它们来平衡新的信号。有很多方法可以做到这一点。将增益应用于新信号短时功率谱的频率上,然后在时域重新合成信号。应用于每个频率的增益与其相应的传递系数的倒数成正比,该系数上升到某个指数k。
表2显示了应用从薯片袋导出的均衡器到从同一物体恢复的语音序列的结果。在没有噪声的情况下,k设为1,但广谱噪声压缩了估计的传递系数的范围。使用更大的k可以弥补这一点。在其中一个女性语音示例上手动调整k值,然后将得到的均衡器应用于所有六个语音示例。由于这种均衡是为了提高恢复信号的可信度而不是语音的可理解性,因此使用谱减法来去除噪声。
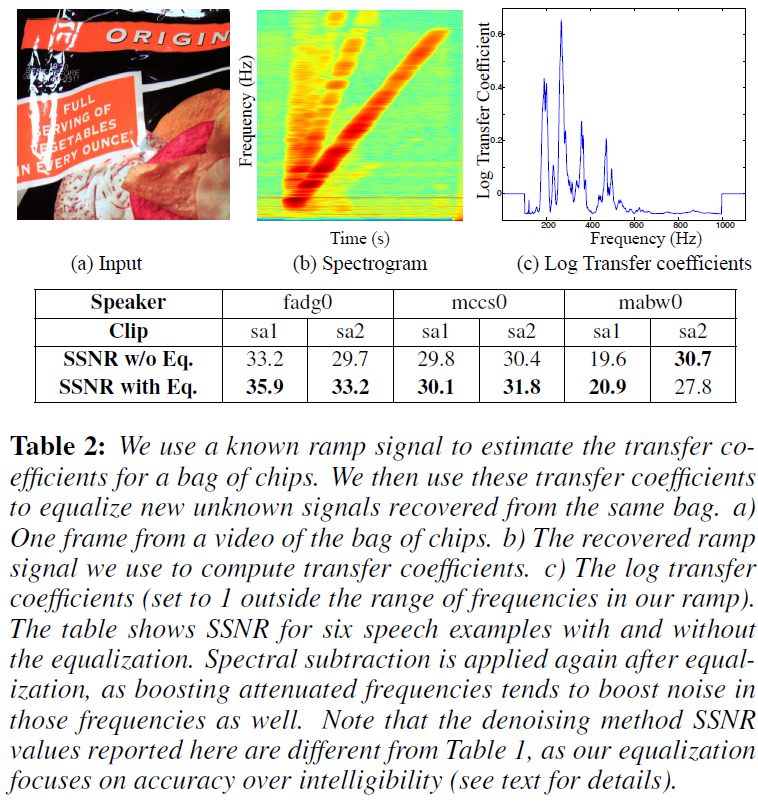
注意,校准和均衡是可选的。特别是,本文中除表2之外的所有结果都假定不预先知道被记录物体的频率响应。
Analysis
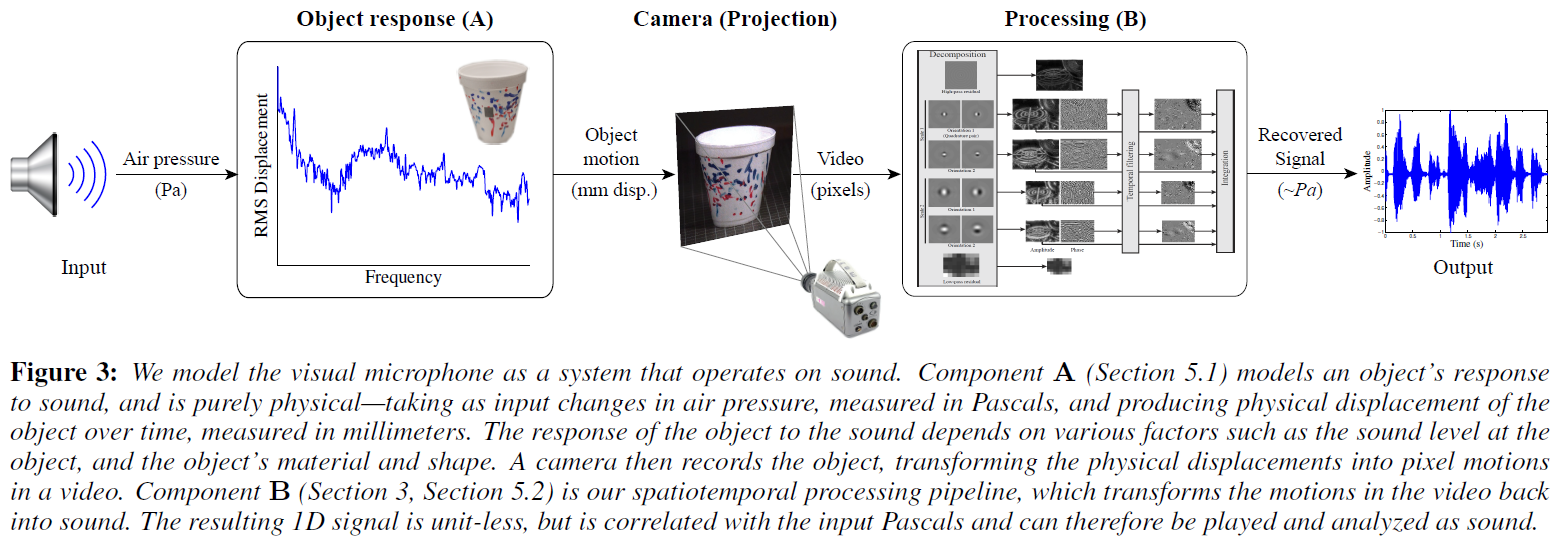
Object response (A): 物体相应声音并移动,将空气压力转化为表面位移。
Processing (B): 将录制的视频转换成恢复的声音。
Object response (A)
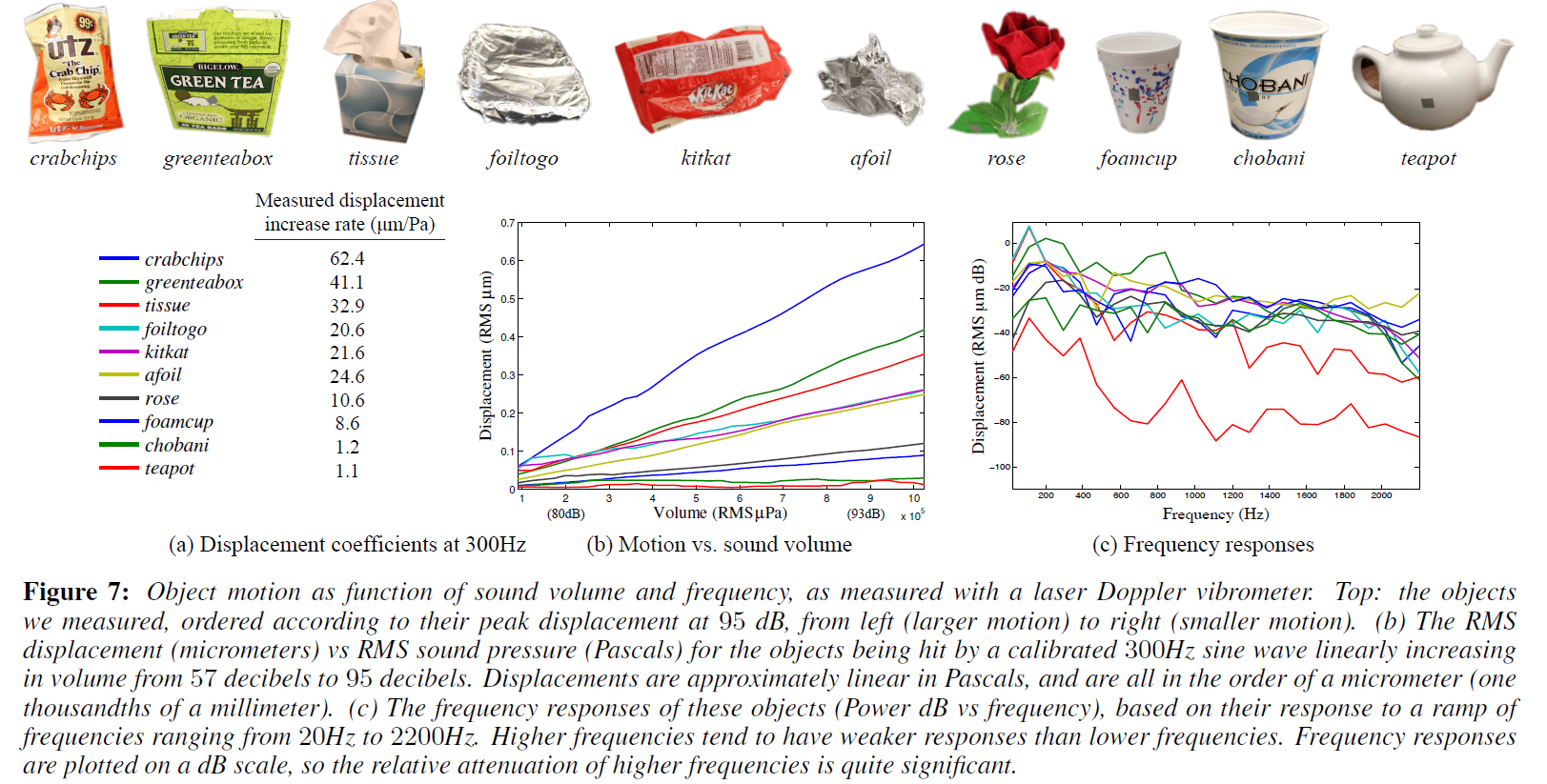
图7(b):300Hz纯音测试,大多数物体的运动在声压(音量)上近似呈线性。结论:A可建模为LTI系统。
图7(c):斜坡信号(20Hz到2200Hz)测试,将A建模为LTI系统,用这个斜坡信号来恢复系统的脉冲响应。这是通过使用维纳反卷积用已知的输入对观察到的斜坡信号(这一次是由LDV记录的)进行反卷积来实现的。图7 (c)显示了从恢复的脉冲响应中得到的频率响应。从这张图中可以看到,大多数物体在低频率的响应比高频率的响应更强(正如预期的那样),但是这种趋势不是单调的。
$\boldsymbol{A}(\omega)$: 转移函数
$S(\omega)$: 声谱
$D_{mm}(\omega)$: 运动谱
项目网址








.png)
.png)
.png)
.png)
.png)
.png)