论文阅读笔记(4)：CNN频域学习(2)

发表于 2020-12-04 更新于 2021-05-17 分类于 Deep Learning Valine：

Faster Neural Networks Straight from JPEG

Motivation

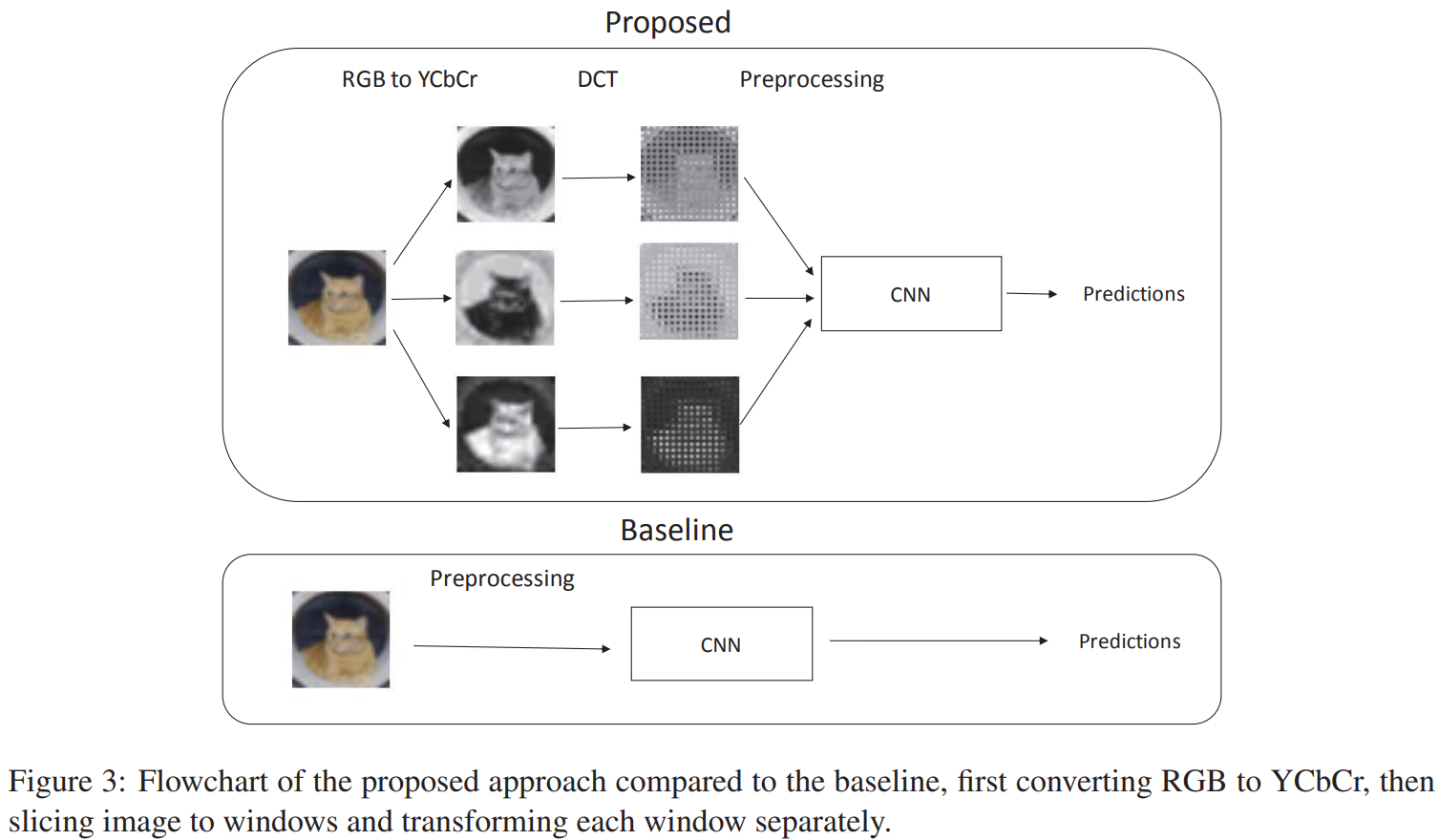
1、缩短图像解码时间。大部分图片都是通过JPEG格式进行存储，JPEG格式转换为RGB需要解码。而如果通过频域学习，解码时只需要从霍夫曼编码中获取DCT系数即可，不需要完全解码得到RGB图像；

2、让模型更高效。CNN模型的优势是表达能力强（参数很多），所需先验少。但是先验少，所以需要大量参数，使得CNN模型中存在大量冗余计算。频域学习其实是一个先验，如果数据分布和该先验一致，那么达到同样的效果，模型可以更简单，所需要的训练数据可以更少。

Method

02_method

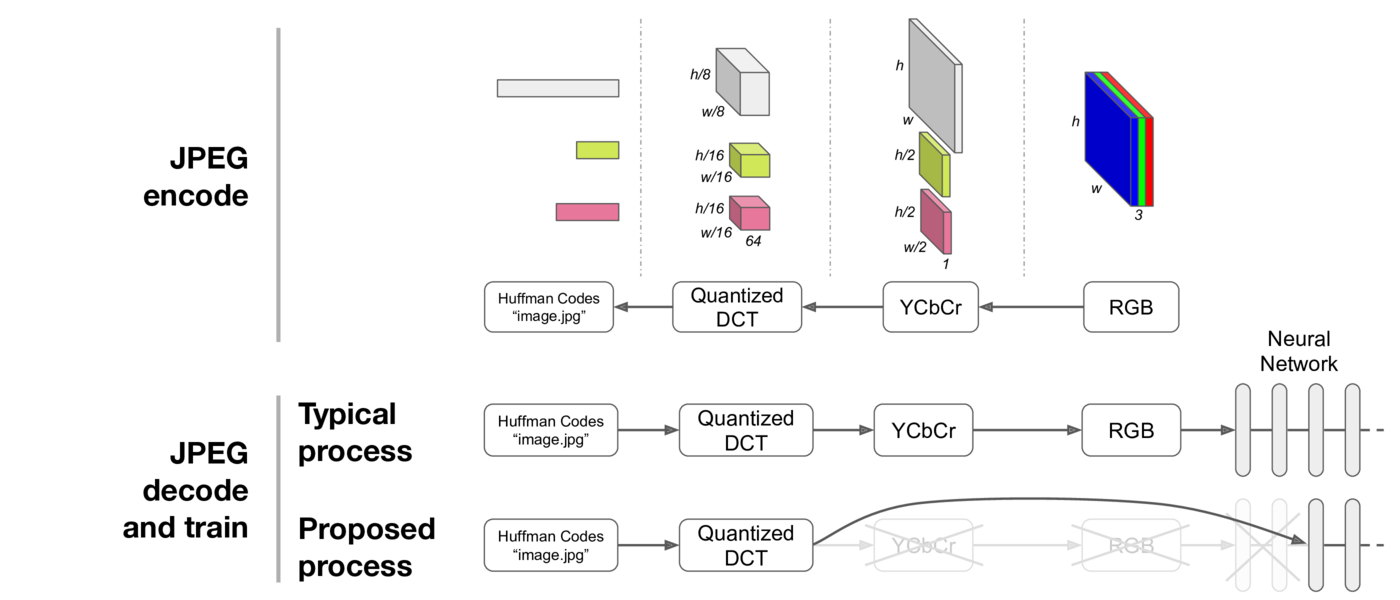
Evaluation

在ImageNet上实验。目标是准确率高且运行速度快。

Baseline

Vanilla ResNet-50, 输入为RGB图像。Top-5错误率7.4%左右，速度200 image/s：

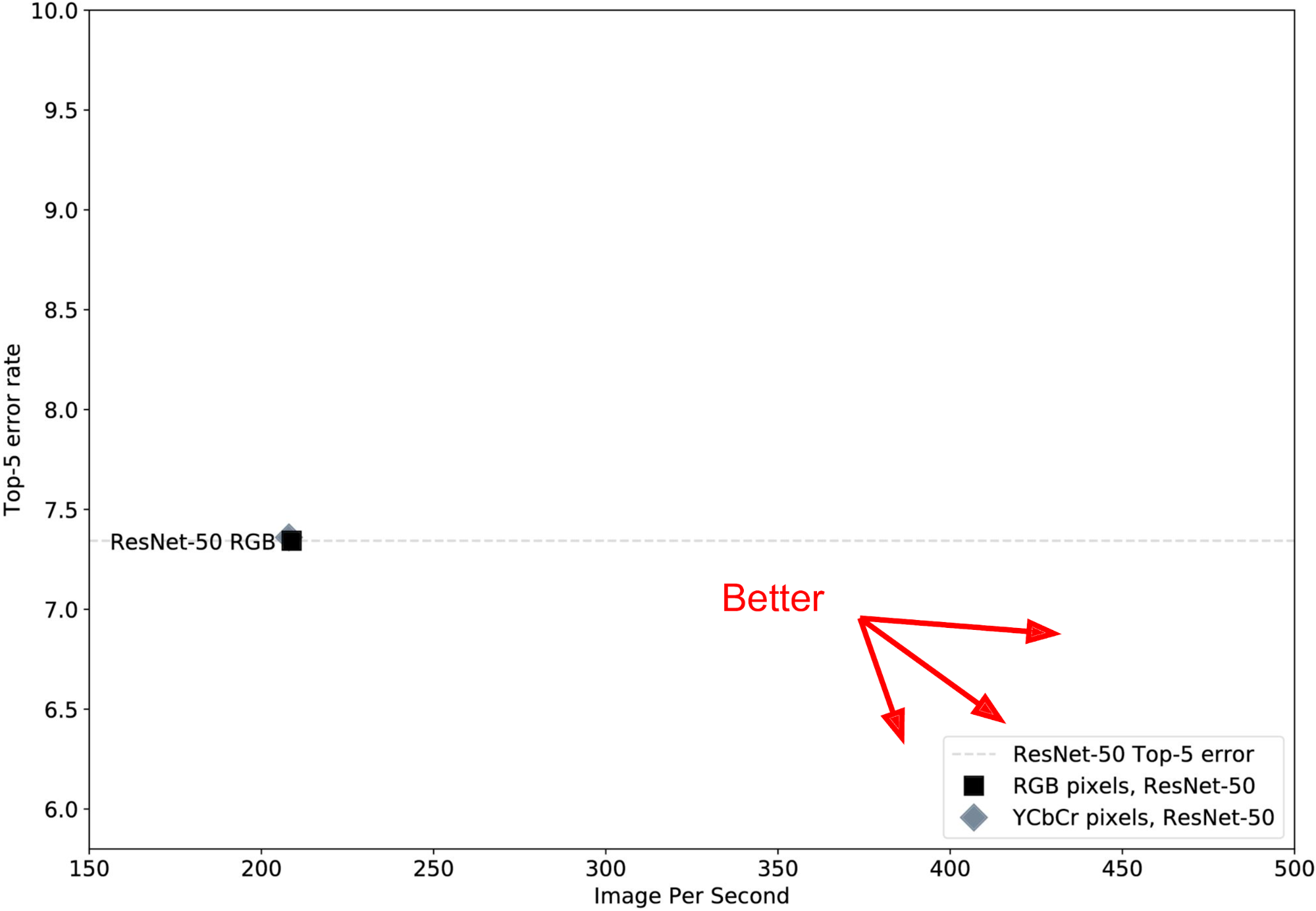
02_result1

以YCbCr为输入，效果与RGB差不多。期望的效果是在图中往右下发展（右：速度快；下：错误率低）。

希望运行速度更快：1）shorter ResNet-50 (减少网络层数)；2）thinner ResNet-50 (减少每层的通道数)

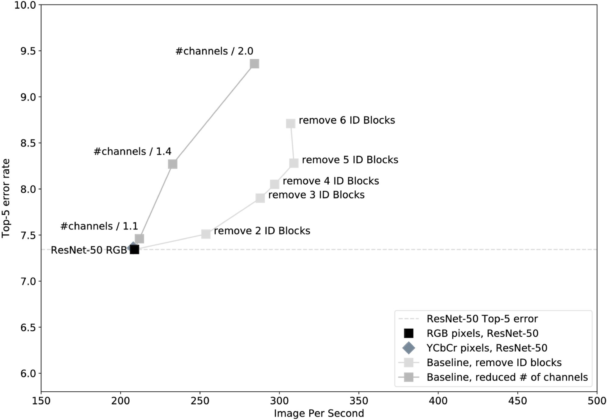
02_result2

结论：shorter ResNet-50优于thinner ResNet-50。浅灰色的“Remove N ID Blocks”的线形成了帕累托前沿(Pareto front)，显示了“non-dominated”网络的集合，或者是那些在速度和准确性之间做出最佳权衡的网络。

Training networks on DCT inputs

问题1：针对不同的输入尺寸如何处理？

RGB图像大小：(224, 224, 3)

DCT系数： 1) Y-(28, 28, 64)；

2) Cb/Cr-(14, 14, 64)

解决：在进入网络之前combine Y和Cb、Cr

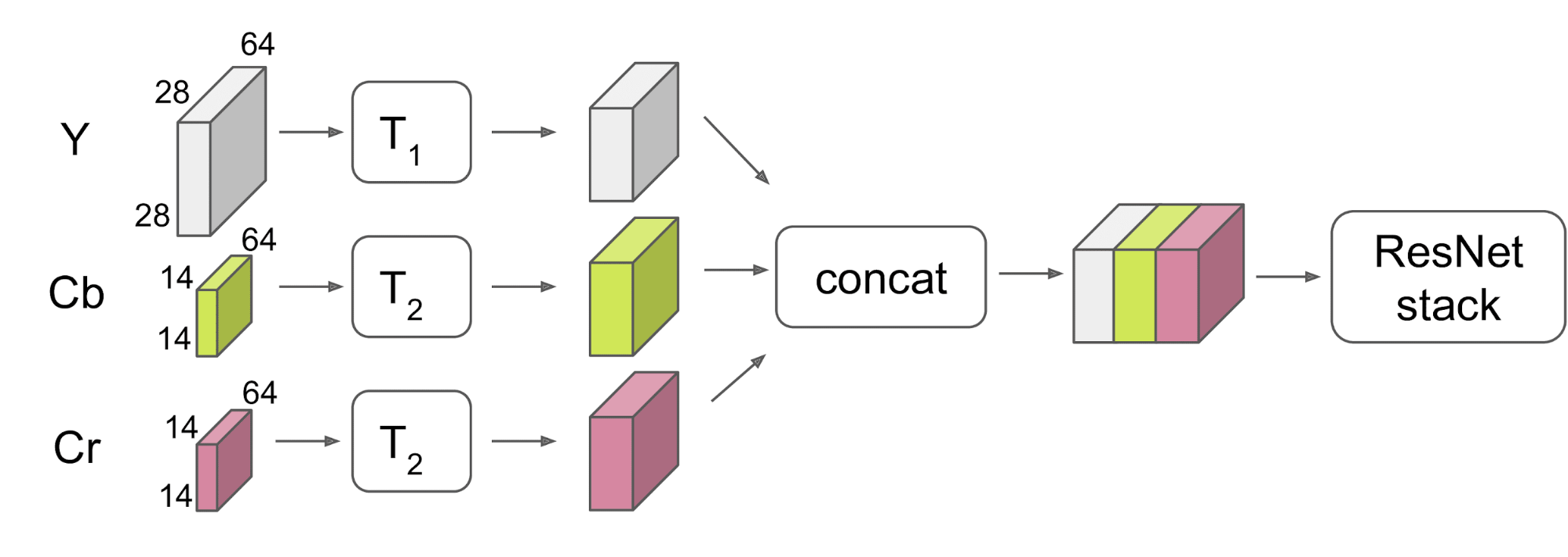
02_net1

1. DCT Early Merge architectures：1）下采Y（“DownSampling”）；2）上采Cb、Cr（“UpSampling”）

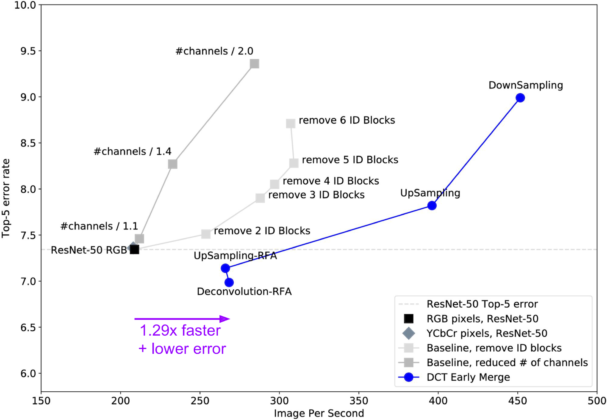
02_result3

结论： 1）DownSampling：fast (450 image/s) but high error；

2） UpSampling：slower but lower error;

问题2：UpSampling的错误率比baseline高

可能的原因：感受野过大。传到baseline ResNet-50的中间层时感受野约为70像素；而UpSampling模型的相应感受野达到了110像素。这是因为DCT输入层的[stride, receptive field]是[8, 8]，而经典输入层该值为 [1, 1]。直观地说，要求网络学习110px宽的感受野，但没有给它足够的层或计算能力来做到这一点。

解决：创造了一个Receptive Field Aware (RFA) 模型→UpSampling-RFA。做法是给神经网络的前层增加额外的步长1模块。此时逐层的感受野增长变得更平滑，近似与baseline ResNet-50相匹配。

如果UpSampling通过可学反卷积而非像素复制得到，则错误率可以进一步降低，达到目前为止最好的模型：Deconvolution-RFA（错误率6.98%；加速1.29倍）。

效果：沿着DCT Early Merge线的其他模型现在形成了新的帕累托前沿，在误差和速度的权衡方面超越了以前的模型。

2. DCT Late Merge architectures

实验发现允许亮度分支多层计算才能获得较高的准确率，而色度路径可以在较少的计算层数下不损害准确率。换句话说，1) 将Y通道放到网络的前面，而Cb/Cr信息在中途注入，其效果与 2) 从前面开始全部三个通道的运算一样好，而方法1)节省了计算。

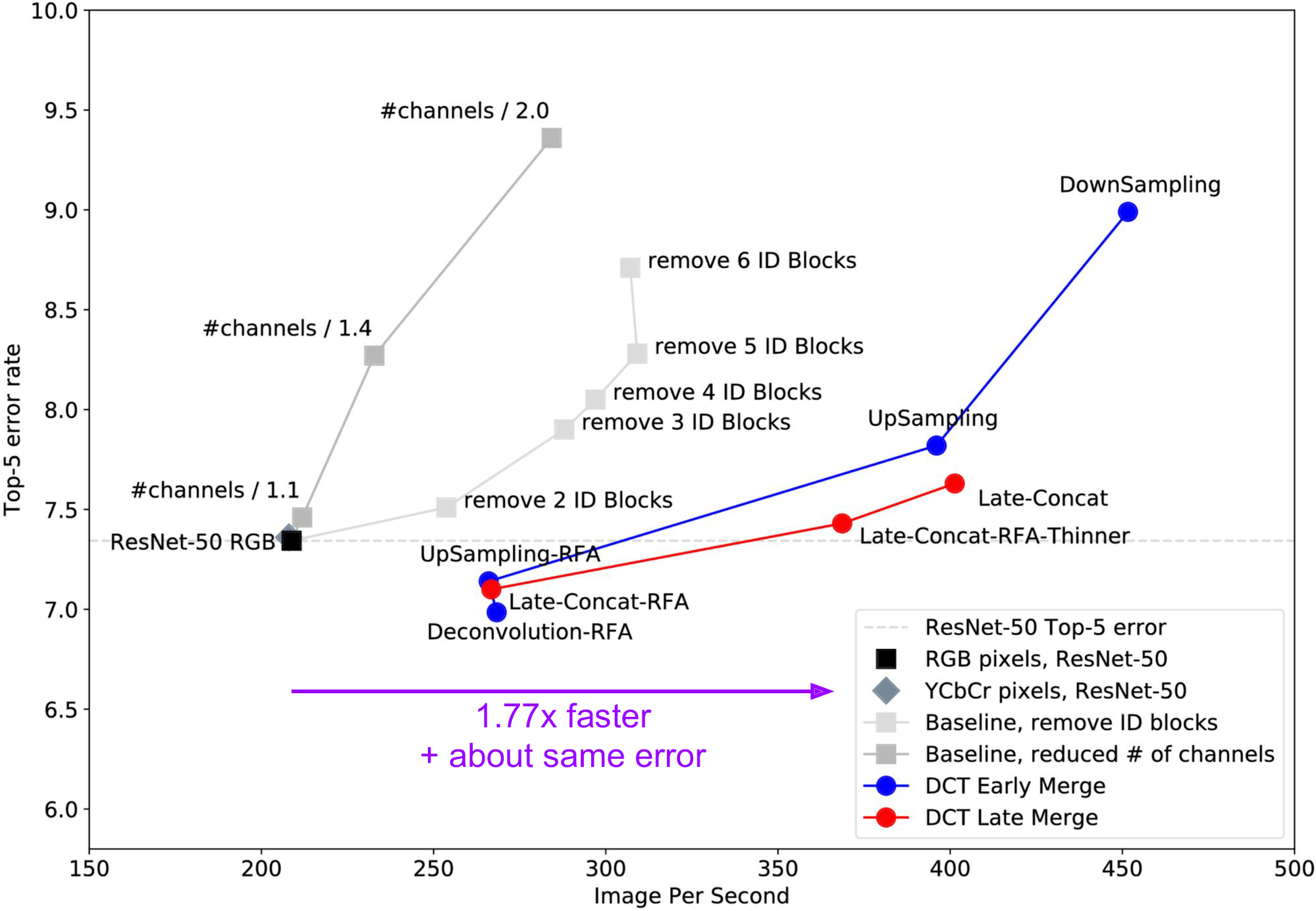
02_result4

Late-Concat-RFA：receptive field aware version；

Late-Concat-RFA-Thinner：通过使用更少过滤器而调整速度的版本。加速1.77倍，错误率相近。

结论：帕累托前沿再次前移。

Discussion

有趣的是，颜色信息在网络后期（当它与从亮度中学到的更高层次的概念相结合时）才被需要。在这一点上猜测可能是学习中级概念（例如:草或狗毛）需要在其与空间上不那么精确的颜色信息（例如:绿色或棕色）结合之前，精细的亮度边缘进行了好几层处理变成纹理。可以从ResNet-50从RGB像素学习到的更高频率的黑白边缘和更低频率（或常数）的颜色检测器中预期这个结果。

02_result5

许多边缘检测器基本上都是黑白的，在亮度空间中操作。许多颜色特征要么在空间上是恒定的，要么在频率上是较低的，它们可能只是用来将粗略的颜色信息传递给需要它的更高层次。我们从2012年就看到过这样的滤波器;我们是否应该期望直到网络后期才需要颜色?

速度与准确率：速度的提升是由于输入层和后续层上的数据量较小。准确率提升的主要原因是 DCT 表示的具体使用，结果对图像分类非常有效。只需将 ResNet-50 的第一个卷积层替换为stride为 8 的DCT 变换，即可获得更好的性能。它甚至比完全相同形状的学习得到的变换（learned transform）效果更好。使用更大的感受野和stride（8）表现更好，而硬编码第一层比学习得到第一层效果更好。残差网络在 2015 年得到 ImageNet 上最先进的性能，只需用DCT 替换第一层，就会进一步提高SOTA。

CNN频域学习博客讲解

Faster Neural Networks Straight from JPEG

Faster Neural Networks Straight from JPEG 博客讲解

论文阅读笔记(3)：CNN频域学习(1)

发表于 2020-12-03 更新于 2021-05-17 分类于 Deep Learning Valine：

On using CNN with DCT based Image Data

Motivation

对于高分辨图像、视频，输入数据量大，CNN运算多→从图像压缩算法JPEG得到启发，经过DCT变换将空域数据转换到频域处理，压缩输入数据量。

Method

01_method

Results

实验数据集：CIFAR10，MNIST

01_result

Discussion

文章直接用DCT系数替代RGB作为CNN输入，处理方法简单直接。Motivation是数据压缩，但是没给出输入数据量减少的实验结果（只是作为future work），而准确率提升也不明显。

On using CNN with DCT based Image Data

论文阅读笔记(2)：AdderNet

发表于 2020-12-02 更新于 2021-05-17 分类于 Deep Learning Valine：

Motivation

目标：设计更加高效的深度神经网络，可以在资源有限的移动设备运行。

现有工作的局限性：常规的卷积基于乘法，代价较高；用二值滤波器替换卷积的工作如BNN等会带来较大的识别准确率下降。

文章思路：常规卷积本质上是一种互相关（输入图像与卷积核之间的相似度度量）。可以用更高效的相似度度量方法来替换常规卷积，使得度量中只包含代价较小的加法操作→AdderNet

AdderNet

开局公式

$Y(m,n,t)=\sum\limits_{i=0}^{d}\sum\limits_{j=0}^{d}\sum\limits_{k=0}^{c_{in}}S(X(m+i,n+j,k),F(i,j,k,t))$

F：卷积核（滤波器）(尺寸$d×d$) 当d=1时，该公式表示全连接层的计算

X：特征图

S：预定义的相似度测量方法，例如互相关中$S(x,y)=x\times y$

从上述公式出发，文章改变S，使用L1距离测量F和X的相似度，使得测量中只有加法没有乘法：

$Y(m,n,t)=-\sum\limits_{i=0}^{d}\sum\limits_{j=0}^{d}\sum\limits_{k=0}^{c_{in}}|X(m+i,n+j,k)-F(i,j,k,t)|$

使用L1距离存在的问题及解决：

问题1：加法滤波器的输出总为负数（会影响激活函数如ReLU的使用）

解决方法：使用Batch Normalization→输出被归一化到适当的范围→CNN中的激活函数在AdderNet中也适用（BN中存在乘法，但是数量太少可以忽略）

问题2.1：优化方法中滤波器F梯度的计算

AdderNet中计算偏微分：

$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)}=sgn(X(m+i,n+j,k)-F(i,j,k,t))$

所以梯度取值只有+1，0，-1。由此进行优化的方法为signSGD，但是，signSGD几乎永远不会沿着最陡的下降方向，并且方向性只会随着维数的增长而变差。

解决方法：使用另一种形式的梯度（实际上是L2范数的梯度）：

$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)}=X(m+i,n+j,k)-F(i,j,k,t)$

问题2.2：优化方法中特征图X梯度的计算

同样使用L2范数的梯度，但是梯度值可能会在[-1，+1]的范围之外→由于chain rule，Y对X的偏导数不仅影响当前层的梯度，还会影响当前层之前的所有层的梯度→梯度爆炸

解决方法：使用HardTanh函数（HT(x)）将X的梯度clip到[-1,+1]的范围。

$\frac{\partial Y(m,n,t)}{\partial X(i,j,k,t)}=HT(F(m+i,n+j,k)-X(i,j,k,t))$

问题3：AdderNet使用L1范数得到的Y方差更大，导致滤波器权重的梯度消失问题

假设F和X服从正太分布

CNN中有

$Var[Y_{CNN}]=\sum\limits_{i=0}^{d}\sum\limits_{j=0}^{d}\sum\limits_{k=0}^{c_{in}}Var[X\times F]=d^{2}c_{in}Var[X]Var[F]$

而AdderNet中则是

$Var[Y_{AdderNet}]=\sum\limits_{i=0}^{d}\sum\limits_{j=0}^{d}\sum\limits_{k=0}^{c_{in}}Var[|X-F|]=(1-\frac{2}{\pi})d^{2}c_{in}(Var[X]+Var[F])$

实际情况中Var[F]非常小，所以$Var[Y_{AdderNet}]$会比$Var[Y_{CNN}]$大。在加法层后面会接一个BN层，大方差会导致X的梯度幅值小，经过chain rule的作用，滤波器的权重梯度幅值会越来越小。

gradient_disappear

解决方法：adaptive learning rate

$\triangle F_{l}=\gamma \times \alpha_{l}\times \triangle L(F_{l})$

$l$：表示第$l$层；$\triangle L(F_{l})$第$l$层F的梯度；$\gamma$：全局学习率

局部学习率：

$\alpha_{l}=\frac{\eta \sqrt k}{||\triangle L(F_{l})||_{2}}$

k：F中的元素数量，用于对L2范数求平均

Results

在MNIST、CIFAR10、CIFAR100、ImageNet上达到与CNN相近的准确率。

v1_imagenet_result

AdderNet的权重服从拉普拉斯分布，而CNN的权重服从高斯分布。

v1_histogram

AdderNet: DoWe Really Need Multiplications in Deep Learning?

AdderNet代码

在Latex中插入python代码

发表于 2020-10-15 更新于 2021-05-17 分类于 Latex Trick Valine：

在Latex中插入Python代码，需要一个第三发的宏包pythonhighlight:

https://github.com/olivierverdier/python-latex-highlighting

下载pythonhighlight.sty后，将它放到你的.tex文件所在目录下。

然后声明要使用pythonhighlight，在tex文件内的导言区：

1 2	\usepackage{graphicx} \usepackage{pythonhighlight}

之后既可以在正文添加代码了:

\begin{python}
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import time
import os
\end{python}

效果如下：

$code$

Hexo+Valine：为博客添加评论

发表于 2020-10-15 更新于 2021-05-17 分类于 Setup Valine：

注册Leancloud账号：https://www.leancloud.cn

注册完以后需要创建一个应用，名字可以随便起，然后 进入应用->设置->应用key

拿到你的appid和appkey之后，打开主题配置文件（我是…\themes\next_config.yml）搜索 valine，填入appid 和 appkey

valine:
  enable: true # When enable is set to be true, leancloud_visitors is recommended to be closed for the re-initialization problem within different leancloud adk version
  appid: XO7jV马赛克zGzoHsz # Your leancloud application appid
  appkey: Amg1Fl马赛克2NfhcO # Your leancloud application appkey
  notify: false # Mail notifier. See: https://github.com/xCss/Valine/wiki
  verify: false # Verification code
  placeholder: Just go go # Comment box placeholder
  avatar: mm # Gravatar style
  guest_info: nick,mail,link # Custom comment header
  pageSize: 10 # Pagination size
  language: # Language, available values: en, zh-cn
  visitor: false # leancloud-counter-security is not supported for now. When visitor is set to be true, appid and appkey are recommended to be the same as leancloud_visitors' for counter compatibility. Article reading statistic https://valine.js.org/visitor.html
  comment_count: true # If false, comment count will only be displayed in post page, not in home page
  #post_meta_order: 0

最后在Leancloud -> 设置 -> 安全中心 -> Web 安全域名把你的域名加进去

刷新一下~ 看到评论框了

删除评论

登录Leancloud>选择你创建的应用>存储>选择ClassComment

参考：

https://blog.csdn.net/blue_zy/article/details/79071414

https://github.com/xCss/Valine/issues/69

PyQt的安装以及在PyCharm上的部署

发表于 2020-05-12 更新于 2021-05-17 分类于 Setup Valine：

PyQt5安装

1 2	pip install pyqt5 pip install pyqt5-tools

第二个命令包含了designer的安装。我的designer.exe安装路径在E:\Anaconda3\Library\bin

可以用Cotana搜索designer，然后右键打开文件所在位置，直接定位它的安装路径，后面要用到。

designer在PyCharm上部署

File->Settings->Tools->External Tools

点击“+”来增加外部工具。

(1) 增加QT设计界面“Qt Designer” — 这个就是设计Qt界面的工具

Program选择PyQt安装目录中 designer.exe 的路径
Work directory 使用变量 $ProjectFileDir$ （点击后面的Insert Macro…）

(2) 增加“PyUIC” — 这个主要是用来将 Qt界面转换成 py代码

Program选择PyQt安装目录中 pyuic5.bat 的路径（我的依然在E:\Anaconda3\Library\bin里）
parameters设置为$FileName$ -o $FileNameWithoutExtension$.py
Work directory 设置为 $ProjectFileDir$ （点击后面的Insert Macro…）

点击确认就设置好了。返回去后通过Tools可以看到：

设计GUI

依照上图，点击PyQt Designer, 在弹出来的界面中选择Wdiget，然后点击创建。

在窗口添加控件，Lable、pushButton、checkBox、lineEdit等：

把.ui文件保存到当前项目目录中，然后右键点击.ui文件：

点击PyUIC即可将.ui转成.py文件。

在login.py中添加：

if __name__=="__main__":
    import sys
    app=QtWidgets.QApplication(sys.argv)
    widget=QtWidgets.QWidget()
    ui=Ui_form()
    ui.setupUi(widget)
    widget.show()
    sys.exit(app.exec_())

运行login.py，就可以看到这个页面了。

QtDesigner的安装

设计GUI

windows更改pip镜像源及解决总是timeout的情况

发表于 2020-05-12 更新于 2021-05-17 分类于 Setup Valine：

pip安装

事情的起因是我想安装PyQt5：

1 2	pip install pyqt5 pip install pyqt5-tools

当然这是最慢的方法，于是可以用镜像源安装：

pip安装使用国内镜像源

清华：https://pypi.tuna.tsinghua.edu.cn/simple

阿里云：http://mirrors.aliyun.com/pypi/simple/

中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/

华中理工大学：http://pypi.hustunique.com/

山东理工大学：http://pypi.sdutlinux.org/ 

豆瓣：http://pypi.douban.com/simple/

临时使用的话加参数-i，例如：

1	pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pyqt5

然而依然总是timeout，于是：

设置pip配置文件

配置文件地址：（如果没有pip.ini文件，就自己新建编辑一个）

1	C:\ProgramData\pip\pip.ini

配置文件内容，将召唤timeout的时长设置得长一些

[global]
timeout = 60
index-url = http://pypi.douban.com/simple
trusted-host = pypi.douban.com
[install]
use-mirrors = true
mirrors = http://pypi.douban.com
trusted-host = pypi.douban.com

设置好之后，再用

1	pip install pyqt5

会显示现在使用的是豆瓣镜像源，速度也飞起来了。

pip安装PyQt5

pip使用国内镜像源

pip配置文件设置

Pytorch计算模型运算量的工具--torchstat

发表于 2020-05-11 更新于 2021-05-17 分类于 PyTorch Tools Valine：

说明与安装

这个包可以计算出一个网络模型的参数量和运算量，甚至给出每一层的运算量，比如：

example

安装方法为：

1	pip install torchstat

示例

import torch
import torch.nn as nn
import torch.nn.functional as F
from torchstat import stat


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(56180, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 56180)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)


if __name__ == '__main__':
    model = Net()
    stat(model, (3, 224, 224))

然后在命令行输入

1	torchstat -f example.py -m Net

如果要更改输入图像的尺寸，只改example.py里的（3，224，224）没有起作用，于是我使用了-s选项：

1	torchstat -f example.py -m Net -s '3x32x32'

这里选项内容是用字符串表示的，‘x’就是字母x。

另一个示例

from torchstat import stat
import torchvision.models as models

model = models.resnet18()
stat(model, (3, 224, 224))

torchstat的Github

论文阅读笔记(1)：NAS之DARTS

发表于 2020-04-26 更新于 2021-05-17 分类于 Deep Learning Valine：

Search Space

搜索cell作为网络结构的构件。cell是包含N个结点的有序序列的有向无环图。结点$x^{(i)}$是隐藏表达（比如卷积网络的特征图），而有向边$(i ,j)$则关联着变换$x^{(i)}$的一些操作$o^{(i,j)}$。文章中假定一个cell中有两个输入节点和一个输出节点。对于卷积cell，输入节点被定义为当前层的前面两层的cell的输出。当前cell的输出是对所有中间节点使用一个压缩操作（比如拼接）得到的。

每一个中间结点基于其所有前向操作计算得到：

$x^{(j)}=\sum_{i<j}o^{(i,j)}(x^{(i)})$

搜索空间中还包含了一个特殊的零操作，表示两个节点之间没有连接。学习cell的任务缩减为学习出cell的各条边的操作类型及参数。

连续优化

O是候选操作（如卷积、最大池化、零操作等）的集合，每个操作表示将一些函数$o(\cdot)$施加到$x^{(i)}$上。为了让搜索空间连续，我们把一个特定操作的范畴选择松弛为所有可能的操作上的一个softmax:

$\overline{o}^{(i,j)}(x)=\sum_{o\in O}\frac{exp⁡(\alpha_{o}^{(i,j)})}{\sum_{o'\in O}exp⁡(\alpha_{o'}^{(i,j)})}o(x)$

对应于节点对$(i, j)$的操作混合权重被参数化为一个维度为|O|（候选操作总个数）的向量$\alpha^{i,j}$。架构搜索的任务就减少为学习一个连续变量集合$\alpha={\alpha^{(i,j)}}$。在搜索的最后，将每个混合操作$\overline{o}^{(i,j)}$用最大似然的操作代替，就可以得到离散化的网络架构。比如$o^(i,j)=argmax_{o\in O}\alpha_{o}^{(i,j)}$在下文中，用$\alpha$表示编码后的架构。

darts

DARTS的cell搜索过程概览如上图所示。该过程总结如下。最开始时cell的各条边的操作类型未知，但是可选的操作类型是预先定义的，候选操作集合中包含以下8种操作：（1）恒等连接；（2）零操作；（3）3×3 深度可分离卷积；(4) 3×3 空洞深度可分离卷积；（5）5×5深度可分离卷积；（6）5×5 空洞深度可分离卷积；（7）3×3平均池化；（8）3×3 最大池化。对于用DAG表示的cell的每条边施加一个候选操作的混合操作（混合操作是上述8种类型操作的混合，输入用8种操作进行处理，对得到的8个输出施以权重$\alpha^{(i.j)}_{o}$，然后松弛化为softmax），从而将分立的搜索空间用softmax函数松弛为连续空间，使得搜索可微分。然后通过求解一个置信优化问题对混合概率和网络权重进行联合优化，最后，将每个混合操作$\overline{o}^{(i,j)}$用最大似然的操作（也就是$i,j$结点的8条边中有着最大权重$\alpha^{(i.j)}_{o}$的那条边所对应的操作）代替，就可以得到离散化的网络架构。也就是说，训练的时候对于每两个结点之间，是8种操作都用到了，用softmax耦合为混合操作。训练完后，只保留了权重最大的那个操作。

现在目标就是将架构$\alpha$和所有混合操作中的权重$w$一起学习出来。DARTS使用梯度下降算法优化交叉检验集损失。使用$L_{train}$和$L_{val}$分别表示训练集loss和交叉检验集的loss，则优化目标是：

$\min\limits_{\alpha}L_{val}(w^{*}(\alpha),\alpha)$ $s.t. w^{*}(\alpha)=argmin_{w}L_{train}(w,\alpha)$

即找到最优结构$\alpha^{*}$使得在验证集上得到最优结果，即最小化$L_{val}(w^{*},\alpha^{*})$，并找到最优参数$w^{*}$，能够在特定结构$\alpha^{*}$上得到最优性能，即最小化$L_{train}(w,\alpha^{*})$。

网络架构梯度近似

由于昂贵的内层优化代价，精确地求出网络架构的梯度是几乎不可能的。因此，这篇文章提出了一个简单的近似方案：

$\bigtriangledown_{\alpha}L_{val}(w^{*}(\alpha),\alpha)\approx\bigtriangledown_{\alpha}L_{val}(w-\xi\bigtriangledown_{w}L_{train}(w,\alpha),\alpha)$

其中$w$是由近似算法得到的当前的权重，$\xi$是一步内层优化的学习率。这个算法的思路是使用一步训练调整得到的$w$来近似$w^{*}(\alpha)$，而不用训练解决内层优化问题直至收敛。如果w已经是内部优化的局部最优值，此时$\bigtriangledown_{w}L_{train}(w,\alpha)=0$，因此等号右边的式子会退化为$\bigtriangledown_{\alpha}L_{val}(w(\alpha),\alpha)$。

算法： algorithm

对近似的架构梯度应用链式法则可以得到：

$\bigtriangledown_{\alpha}L_{val}(w',\alpha)-\xi\bigtriangledown^{2}_{\alpha,w}L_{train}(w,\alpha)\bigtriangledown_{w'}L_{val}(w',\alpha)$

其中$w’=w-\xi\bigtriangledown_{w}L_{train}(w,\alpha)$表示一个一步前向网络的权重值。上式的第二项中包含了一个昂贵的矩阵-向量乘法，但是使用有限差分近似可以显著降低计算复杂度。使用一个很小的数值$\epsilon$，并令$w^{\pm}=w\pm\epsilon\bigtriangledown_{w’}L_{val}(w’,\alpha)$，则：

$\bigtriangledown^{2}_{\alpha,w}L_{train}(w,\alpha)\bigtriangledown_{w'}L_{val}(w',\alpha)\approx\frac{\bigtriangledown_{\alpha}L_{train}(w^{+},\alpha)-\bigtriangledown_{\alpha}L_{train}(w^{+},\alpha)}{2\epsilon}$

计算这个有限差分式只需要权重值的两个前传项和$\alpha$的两个反传项，计算复杂度从$O(|\alpha||w|)$降到$O(|\alpha|+|w|)$。

一阶近似：

当$\xi = 0$时，式(7)中的二阶导数项会消失。此时，架构梯度由$\bigtriangledown_{\alpha}L_{val}(w,\alpha)$给出，对应着假定当前的$w$与$w^{*}(\alpha)$相同然后优化交叉检验loss的情况。这会带来一些加速，但是根据实验结果显示，性能会变差。下文用一阶近似来指代$\xi = 0$的情形，用二阶近似来指代$\xi > 0$时的梯度公式。

离散架构推导

为了组成离散架构中的每一个节点，文中在该节点所有的前面节点的所有的非零候选操作中保留了top-k的最强操作。一个操作的强度被定义为

$\frac{exp(\alpha^{(i,j)}_o)}{\sum\limits_{o'\in O}exp(\alpha^{(i,j)}_{o'})}$

其实就是两个节点之间所有候选操作都施加上去，给每个候选操作都赋予权值。权值用softmax激活之后相加起来作为节点的输出，反传学习可以更新结构权值$\alpha$。最后保留权重最大的（强度最强的）k个结点与本结点的连接。在DARTS的文章中，CNN中选择k=2。

DARTS论文

具体公式推导